本文主要记录在三维空间的物体转换为二维图像的过程，即相机的投影过程。

一、小孔成像模型与坐标系

相机的拍摄过程可以简化为小孔成像的一种形式，利用这种形式很容易就能得到相机模型中的数学表达式。通过相机的成像方式及其数学表达式，可以看出三维场景和图像中每一个像素之间的映射关系。

相机的模型结构如下图所示，为了使其简单化，把成像的平面置于小孔前面，并且拍摄出来的图像也应该是正立的。

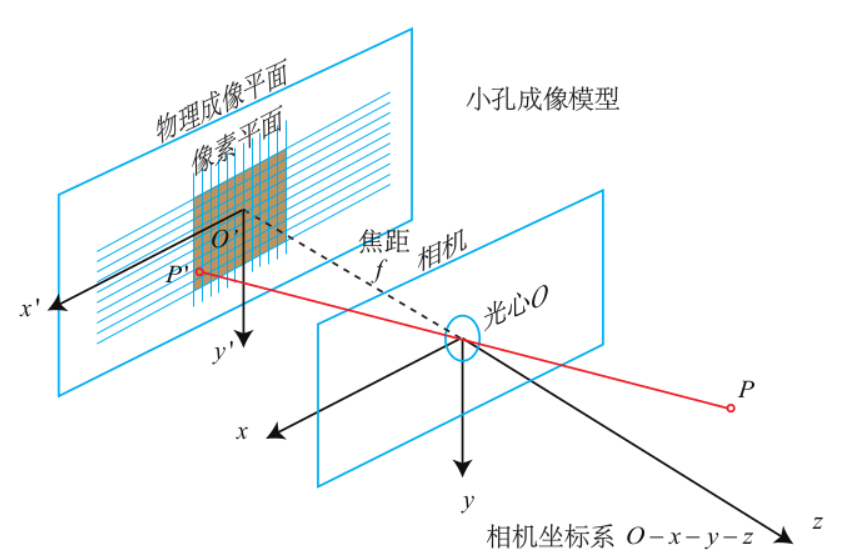
在小孔成像模型中，场景从三维空间投影到图片上的整个过程可以理解为三个步骤和四个坐标系。

具体流程如下：从世界坐标系转换到相机坐标系，再从相机坐标系转换到图像坐标系，最后从图像坐标系转换到像素坐标系。

四个坐标系的定义如下：

世界坐标系：一个客观的绝对存在，世界坐标系都需要预先确定，指定其原点和方向。在定义好的世界坐标系中可以放置任何物体。世界坐标系下的坐标通常用（Xw,Yw,Zw）来进行表示。
相机坐标系：目前通用的定义方法是以一台相机的光心或者主点作为坐标系的原点。X轴和Y轴在拍摄画面时分别平行于图像的横轴和纵轴，Z轴为相机的焦距所指方向。相机坐标系下的坐标通常使用符号（Xc,Yc,Zc）来进行表示。
图像坐标系：根据图像进行定义，以图象中心作为原点，X 轴和 Y 轴与相机的 X 轴和 Y 轴的方向保持一致。图像坐标是使用米、厘米等物理学单位来表示的坐标系。图像坐标系只有两个维度，没有Z轴。图像坐标系下通常使用符号（x, y）来表示。
像素坐标系：以像素为单位的坐标系。像素坐标系也是二维坐标系，其 X 轴和 Y 轴的方向与图像坐标系一致。坐标原点位于二维图像的左上角。像素通用的表示形式为一个方块或者矩形，每个像素里面存放的信息为像素的强度和灰度值。

二、坐标系的转换

在第一小节中，已经定义了各个坐标系及其表示形式，在该小节中，将通过数学模型的形式，推导小孔成像的过程。整个过程分为三个步骤，其中世界坐标系到相机坐标系的变化过程涉及相机的外参，从相机的坐标系转换到图像坐标系再转换到像素坐标系的过程中都涉及到了相机的内参的使用。该小节通过相机内参以及外参的形式推导相机的投影过程。

(1) 相机外参

世界坐标系（Xw,Yw,Zw）与相机坐标系（Xc,Yc,Zc）的转换。

假设点 P 是一个三维空间的点，其在相机坐标系下的位置为 Pc ，在世界坐标系下的位置为 Pw 。Pw 和 Pc 可以通过一个变换矩阵相互转换，该变换矩阵可以细分为旋转矩阵(R)和平移矩阵(t).其数学表达式为：

$P_c=RP_w+t$

其中 R 有三个自由度，是一个 3 * 3 的矩阵，表示相机在世界坐标系下的旋转。t 表示相机的原点（或者说相机开始时的坐标系的原点）相对于世界坐标系的变化，是一个 3 * 1的矩阵。上式可以展开为：

$\begin{bmatrix} X_c \\ Y_c \\ Z_c \\ \end{bmatrix} = \begin{bmatrix} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} \\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ \end{bmatrix} + \begin{bmatrix} t_1 \\ t_2 \\ t_3 \\ \end{bmatrix}$

其齐次方程表的形式可以表示为：

$\begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \\ \end{bmatrix} = \begin{bmatrix} R_{11} & R_{12} & R_{13} & t_1\\ R_{21} & R_{22} & R_{23} & t_2\\ R_{31} & R_{32} & R_{33} & t_3\\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \\ \end{bmatrix}$

可以简化为：

$\begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \\ \end{bmatrix} = \begin{bmatrix} \mathbf{R} & \mathbf{t} \\ \mathbf{0} & 1\\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \\ \end{bmatrix}$

(2) 相机内参

相机坐标系(Xc, Yc, Zc)与图像坐标系(x, y)的转换：相机坐标系是一个三维坐标系，图像坐标系是二维坐标系，三维到二维有一个降维的过程，主要是丢掉了深度这一维度，坐标向量由三维转为二维。

如下图，相机坐标系下存在任一点，图像上的坐标点与该三维点对应。由于两个坐标系的 X轴、Y轴一致，因此可以增加一个维度 f，形成相机坐标系的坐标，其中 f 是相机的焦距。

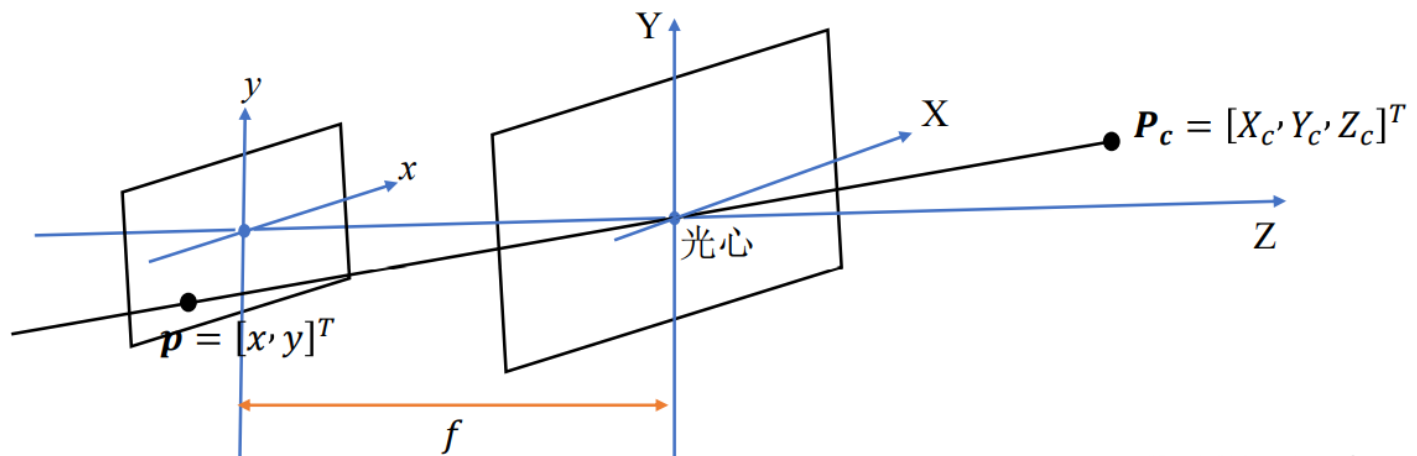
由相似三角形，可得以下公式：

$\frac{z_c}{f} = \frac{x_c}{f} = \frac{y_c}{f}$

整理可得：

$\left\{\begin{array}{cc} x=f\frac{x_c}{z_c} \\ y=f\frac{y_c}{z_c} \\ z=f \\ \end{array}\right.$

转化为齐次坐标系下为：

$Z_c · \begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix} = \begin{bmatrix} f & 0 & 0 & 0\\ 0 & f & 0 & 0\\ 0 & 0 & 1 & 0\\ \end{bmatrix} · \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \\ \end{bmatrix}$

至此推导出了相机坐标系与图像坐标系的转换数学模型。

图像坐标系与像素坐标系的转换：这两个坐标系最核心的区别在于其单位不一致。

如下图：O为像素坐标系原点，O1为图像坐标系原点

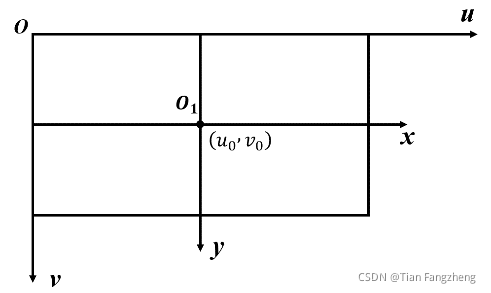
假设(u~0~, v~0~)为像素坐标系下的坐标，表示整个图像的中心。像素的表示形式通常为矩形或是长方形，设像素的长宽分别为dx 、dy 。有对应关系可得：

$\left\{\begin{array}{cc} u=\frac{x}{dx}+u_0\\ v=\frac{y}{dy}+v_0 \\ \end{array}\right.$

转换到齐次坐标系得：

$\begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \begin{bmatrix} \frac{1}{dx} & 0 & u_0 \\ 0 & \frac{1}{dy} & v_0 \\ 0 & 0 & 0 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix}$

到此为之，得到了图像坐标系（x, y）到像素坐标系（u, v）的转换的数学模型。

结合（7）、（9）得到一个三维空间中的点从相机坐标系到像素坐标系的整个投影过程，其数学表达式如下：

$Z_c · \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \begin{bmatrix} f_x & 0 & u_0 & 0\\ 0 & f_y & v_0 & 0\\ 0 & 0 & 1 & 0\\ \end{bmatrix} · \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \\ \end{bmatrix}$

其中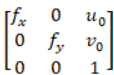被称为相机的内参矩阵，用K表示。

内参矩阵 K 有4个未知的数据，这四个数据与相机的构造相关。$f_x, f_y$ 为 $\frac{f}{dx}$, $\frac{f}{dy}$ 的简写形式，f 表示相机的焦距，$dx,dy$ 是单位像素的长和宽。$u_0, v_o$ 是像素坐标系下图像中间未知的坐标。

（3) 内外参数组合

通过相机的内参和外参，可以将相机模型中的四个坐标系之间的变换全部联系起来，其数学形式为：

$Z_c · \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \begin{bmatrix} f_x & 0 & u_0 & 0\\ 0 & f_y & v_0 & 0\\ 0 & 0 & 1 & 0\\ \end{bmatrix} \begin{bmatrix} \mathbf{R} & \mathbf{t} \\ \mathbf{0} & 1\\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \\ \end{bmatrix}$

三、参考资料

主要参考：https://blog.csdn.net/TFZ941214/article/details/121235284

关于计算摄影学：https://zhuanlan.zhihu.com/p/570452119